Bernoulli process

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables X_i are identical and independent. Prosaically, a Bernoulli process is repeated coin flipping, possibly with an unfair coin with consistant unfairness.

Every variable X_i in the sequence may be associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution.

The problem of determining the process, given only a limited sample of the Bernoulli trials, may be called the problem of checking if a coin is fair.

1 Definition
- 1.1 Interpretation
2 Formal definition
3 Bernoulli sequence
4 Randomness extraction
5 Generalizations
6 See also
7 References
8 External Links

Definition

A Bernoulli process is a finite or infinite sequence of independent random variables X₁, X₂, X₃, ..., such that

For each i, the value of X_i is either 0 or 1;
For all values of i, the probability that X_i = 1 is the same number p.

In other words, a Bernoulli process is a sequence of independent identically distributed Bernoulli trials.

Independence of the trials implies that the process is memoryless. Given that the probability p is known, past outcomes provide no information about future outcomes. (If p is unknown, however, the past informs about the future indirectly, through inferences about p.)

If the process is infinite, then from any point the future trials constitute a Bernoulli process identical to the whole process, the fresh-start property.

Interpretation

The two possible values of each X_i are often called "success" and "failure". Thus, when expressed as a number 0 or 1, the outcome may be called the number of successes on the ith "trial".

Two other common interpretations of the values are true or false and yes or no. Under any interpretation of the two values, the individual variables X_i may be called Bernoulli trials with parameter p.

In many applications time passes between trials, as the index i increases. In effect, the trials X₁, X₂, ... X_i, ... happen at "points in time" 1, 2, ..., i, .... That passage of time and the associated notions of "past" and "future" are not necessary, however. Most generally, any X_i and X_j in the process are simply two from a set of random variables indexed by {1, 2, ..., n} or by {1, 2, 3, ...}, the finite and infinite cases.

Several random variables and probability distributions beside the Bernoullis may be derived from the Bernoulli process:

The number of successes in the first n trials, which has a binomial distribution B(n, p)
The number of trials needed to get r successes, which has a negative binomial distribution NB(r, p)
The number of trials needed to get one success, which has a geometric distribution NB(1, p), a special case of the negative binomial distribution

The negative binomial variables may be interpreted as random waiting times.

Formal definition

The Bernoulli process can be formalized in the language of probability spaces as a random sequence in {0, 1}, a single random variable.

A Bernoulli process is then a probability triple 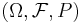$(\Omega, \mathcal{F}, P)$ and a random variable X mapping Ω into the set {0, 1}^N such that for every 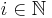$i \in\mathbb{N}$ , one has 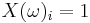$X(\omega)_i=1$ with probability p and 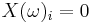$X(\omega)_i=0$ with probability 1 − p.

Where there is no possible confusion, X_i(ω) may be written X_i.

Bernoulli sequence

The term Bernoulli sequence is often used informally to refer to a realization of a Bernoulli process. However, the term has an entirely different formal definition as given below.

Suppose a Bernoulli process formally defined as a single random variable (see preceding section). For every 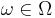$\omega \in \Omega$ there is a sequence of integers

$\mathbb{Z}^\omega = \{n\in \mathbb{Z}�: X_n(\omega) = 1 \} \,$

called the Bernoulli sequence associated with the Bernoulli process. For example, if ω represents a sequence of coin flips, then the associated Bernoulli sequence is the list of natural numbers or time-points for which the coin toss outcome is heads.

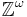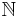So defined, a Bernoulli sequence $\mathbb{Z}^\omega$ is also a random subset of the index set, the natural numbers $\mathbb{N}$ .

Almost all Bernoulli sequences 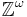$\mathbb{Z}^\omega$ are ergodic sequences.

Randomness extraction

Main article: Randomness extractor

From any Bernoulli process one may derive a Bernoulli process with p = 1/2 by the von Neumann extractor, the earliest randomness extractor, which actually extracts uniform randomness.

Represent the observed process as a sequence of zeroes and ones, or bits, and group that input stream in non-overlapping pairs of successive bits, such as (11)(00)(10)... . Then for each pair,

if the bits are equal, discard;
if the bits are not equal, output the first bit.

This table summarizes the computation.

input	output
00	discard
01	0
10	1
11	discard

In the output stream 0 and 1 are equally likely, as 10 and 01 are equally likely in the original, both having probability pq = qp. This extraction of uniform randomness does not require the input trials to be independent, only uncorrelated. More generally, it works for any exchangeable sequence of bits: all sequences that are finite rearrangements are equally likely.

The Von Neumann extractor uses two input bits to produce either zero or one output bits, so the output is shorter than the input by a factor of at least 2. On average the computation discards proportion p² + (1 − p)² of the input pairs, or proportion p² + q², which is near one when p is near zero or one.

The discard of input pairs is at least proportion 1/2, the minimum which occurs where p = 1/2 for the original process. In that case the output stream is 1/4 the length of the input on average.

Generalizations

The generalization of the Bernoulli process to more than two possible outcomes is called the Bernoulli scheme.

References

Carl W. Helstrom, Probability and Stochastic Processes for Engineers, (1984) Macmillan Publishing Company, New York ISBN 0-02-353560-1.
Dimitri P. Bertsekas and John N. Tsitsiklis, Introduction to Probability, (2002) Athena Scientific, Massachusetts ISBN 1-886529-40-X

External Links

Using a binary tree diagram for describing a Bernoulli process